Ювелирное обозрение

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Второй закон Ньютона для такого осциллятора запишется в виде: 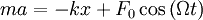. Если ввести обозначения: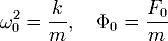и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение: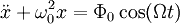

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид: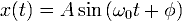

где A,φ произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида: 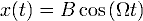и получим значение для константы:

Тогда окончательное решение запишется в виде: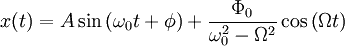

Резонаìнс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Увеличение амплитуды – это лишь следствие резонанса, а причина – совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: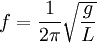

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

Р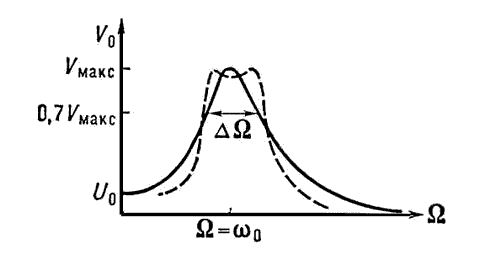езонансная кривая колебательного контура Резонансная кривая колебательного контура: w0 — частота собственных колебаний; W — частота вынужденных колебаний; DW — полоса частот вблизи w0, на границах которой амплитуда колебаний V = 0,7 Vmakc. Пунктир — резонансная кривая двух связанных контуров.

26. Основные понятия и исходные положения положения термодинамики. Обратимые и необратимые процессы. Круговые процессы (циклы).

Термодинамика – раздел физики, изучающий соотношения и превращения теплоты и других форм энергии

Перечень начал термодинамики

Первое начало термодинамики представляет собой закон сохранения энергии в применении к термодинамическим системам.( Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил)

Второе начало термодинамики накладывает ограничения на направление термодинамических процессов, запрещая самопроизвольную передачу тепла от менее нагретых тел к более нагретым. Также формулируется как закон возрастания энтропии. dS≥0 (Неравенство Клаузиуса)

Третье начало термодинамики говорит о том, как энтропия ведет себя вблизи абсолютного нуля температур.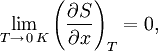

Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.

Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.

Обратимые процессы дают наибольшую работу. Боìльшую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.

Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, теплопроводность и др.

Термодинамиìческие циìклы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия) совпадают.

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, циклы Стирлинга и Эрикссона), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора

Явление резонанса заключается в том, что амплитуда устано­вившихся вынужденных колебаний достигает наибольшего зна­чения, когда частота вынуждающей силы равна собственной час­тоте колебательной системы.

Отличительной особенностью вынужденных колебаний явля­ется зависимость их амплитуды от частоты изменения внешней силы. Для изучения этой зависимости можно воспользоваться установкой, изображенной на рисунке:

На кривошипе с ручкой укреплен пружинный маятник. При равномерном вращении руч­ки на груз через пружину передается действие периодически изменяющейся силы. Изменяясь с частотой, равной частоте враще­ния ручки, эта сила заставит груз совершать вынужденные колебания. Если вращать ручку кривошипа очень медленно, то груз вместе с пружиной будет перемещаться вверх и вниз так же, как и точка подвеса О. Амплитуда вынужденных колебаний при этом будет невелика. При более быстром вращении груз начнет колебаться сильнее, и при частоте вращения, равной собственной частоте пружинного маятника (ω = ω_соб), амплитуда его колебаний достигнет максимума. При дальнейшем увеличении частоты вра­щения ручки амплитуда вынужденных колебаний груза опять станет меньше. Очень быстрое вращение ручки оставит груз почти неподвижным: из-за своей инертности пружинный маятник, не успевая следовать изменениям внешней силы, будет просто дро­жать на месте.

Явление резонанса можно продемонстрировать и с нитяными маятниками. Подвесим на рейке массивный шар 1 и несколько ма­ятников, имеющих нити разной длины. Каждый из этих маятников имеет свою собственную частоту колебаний, которую можно определить, зная длину нити и ускорение свободного падения.

Теперь, не трогая легких маятников, выведем шар 1 из положения равновесия и отпустим. Качания массивного шара вызовут периодические колебания рейки, вследствие которых на каждый из легких маятников начнет действовать периодически изменяющаяся сила упругости. Частота ее изменений будет равна частоте колебаний шара. Под действием этой силы маятники начнут совершать вынужденные колебания. При этом маятники 2 и 3 останутся почти неподвижными. Маятники 4 и 5 будут колебаться с немного большей амплитудой. А у маятника б, имеющего такую же длину нити и, следовательно, собственную частоту колебаний, как у шара 1, амп­литуда окажется максимальной. Это и есть резонанс.

Резонанс возникает из-за того, что внешняя сила, действуя в такт со свободными колебаниями тела, все время совершает положительную работу. За счет этой работы энергия колеблющегося тела увеличивается, и амплитуда колебаний возрастает.

Резкое возрастание амплитуды вынужденных колебаний при ω = ω_соб называется резонансом.

Изменение амплитуды колебаний в зависимости от частоты при одной и той же амплитуде внешней силы, но при различных коэффициентах трения и, изображено на рисунке ниже, где кривой 1 соответствует минималь­ное значение и, кривой 3 — максимальное.

Из рисунка видно, что о резонансе имеет смысл говорить, если зату­хание свободных колебаний в системе мало. Иначе амплитуда вынужден­ных колебаний при ω = ω мало отличается от амплитуды колебаний при других частотах.

Явление резонанса в жизни и в технике.

Явление резонанса может играть как положительную, так и отрицательную роль.

Известно, например, что тяжелый «язык» большого колокола может раскачать даже ребенок, но при условии, что будет тянуть за веревку в такт со свободными колебаниями «языка».

На применении резонанса основано действие язычкового частотомера. Этот прибор представляет собой набор укрепленных па общем основании упругих пластин различной длины. Собствен­ная частота каждой пластины известна. При контакте частотомера с колебательной системой, частоту которой нужно определить, с наибольшей амплитудой начинает колебаться та пластина, частота которой совпадает с измеряемой частотой. Заметив, какая пластина вошла в резонанс, мы определим частоту колебаний системы.

С явлением резонанса можно встретиться и тогда, когда это совершенно нежелательно. Так, на­пример, в 1750 г. близ города Анжера во Франции через цепной мост длиной 102 м шел в ногу отряд солдат. Частота их шагов совпала с частотой свободных колебаний моста. Из-за этого размахи ко­лебаний моста резко увеличились (наступил резонанс), и цепи оборвались. Мост обрушился в реку.

В 1830 г. по той же причине обрушился подвесной мост около Манчестера в Англии, когда по нему маршировал военный отряд.

В 1906 г. из-за резонанса разрушился Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон.

Теперь для предотвращения подобных случаев войсковым частям при переходе через мост приказывают «сбить ногу», идти не строевым, а вольным шагом.

Если же через мост проезжает поезд, то, чтобы избежать резонанса, он проходит его либо на медленном ходу, либо, наоборот, на максимальной скорости (чтобы частота ударов колес о стыки рельсов не оказалась равной собственной частоте моста).

Собственной частотой обладает и сам вагон (колеблющийся на своих рессорах). Когда частота ударов его колес на стыках рельсов оказывается ей равной, вагон начинает сильно раскачиваться.

Явление резонанса встречается не только на суше, но и в море, и даже в воздухе. Так, например, при некоторых частотах гребного вала в резонанс входили целые корабли. А на заре разви­тия авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания частей самолета, что он разваливался в воздухе.

Явления резонанса связаны с периодическим колебательным движением электронов в контуре и состоят в том, что электроны в данном колебательном контуре легче всего «раскачиваются» с какой-то определенной частотой, которую мы называем резонансной. С периодическим колебательным движением мы встречаемся повсеместно. Колебания маятника, дрожание струны, движение качелей — все это примеры колебательного движения.

Для примера рассмотрим колебательную систему, изображенную на рисунке 1. Эта система, как мы увидим дальше, имеет много общего с электрическим колебательным контуром. Состоит она из пружины и массивного шара, закрепленного на стержне.

Рисунок 1. Механическая модель колебательного контура. Масса-индуктивность, гибкость-емкость, трение-сопротивление.

Если мы оттянем шар в низ от положения равновесия, то он под действием пружины немедленно устремится обратно; однако приобретя некоторую скорость шар не остановится в точке равновесия, а по инерции проскочит дальше, чем вызовет новую деформацию (сжатие) пружины. Затем этот процесс повторится в обратном направлении и т. д. Шар будет колебаться в ту и другую сторону до тех пор, пока не израсходуется на трение весь запас энергии, сообщенной пружине при отклонении шара.

Нетрудно заметить, что при колебаниях шара энергия, сообщенная системе, все время переходит из энергии деформации (сжатия и растяжения) пружины в энергию движения шара и обратно. В механике первый вид энергии называется потенциальной энергией, а второй вид — кинетической.

В то время, когда шар находится в одном из крайних положений, он на мгновение останавливается. В этот момент энергия его движения равна нулю. Зато пружина в этот момент очень сильно деформирована: или сжата или растянута; в ней, следовательно, заключено наибольшее количество энергии. В тот же момент, когда шар с наибольшей скоростью проходит через положение равновесия, он обладает наибольшей энергией, но зато энергия пружины в этот момент равна нулю, так как она не сжата и не растянута.

Отклоняя шар на различные расстояния и наблюдая каждый раз за частотой последующих свободных колебаний системы, мы заметим, что частота колебаний системы остается все время одной и той же. Иными словами, она не зависит от величины начального отклонения. Эту частоту мы будем называть собственной частотой колебаний системы.

Если бы мы имели в своем распоряжении не одну такую систему, а несколько, то мы могли бы убедиться в том, что собственная частота свободных колебаний системы уменьшается с увеличением массы шара и увеличивается с увеличением упругости, т. е. с уменьшением гибкости пружины. Эта зависимость может быть обнаружена и на более простом примере с колеблющимися струнами различной толщины и различной степени натяжения.

Если мы пожелаем раскачать шар с наименьшей затратой усилий, то мы, безусловно, постараемся, во-первых, установить строгую периодичность наших толчков, т. е. постараемся, чтобы толчки следовали друг за другом через определенное время, а во-вторых, постараемся, чтобы промежуток времени между толчками равнялся периоду собственных колебаний системы (Рисунок 2).

Рисунок 2. Механическая модель колебательного контура с незатухающими колебаниями. Частота вынужденной силы равна собсвенной частоте системы (резонанс).

Для того чтобы раскачать колебательную систему с наименьшей затратой усилий, нужно частоту вынуждающей силы сделать равной собственной частоте колебания системы. Это правило очень хорошо известно всем нам еще с детского возраста, когда мы его применяли, раскачиваясь на качелях.

Рисунок 3. Явление резонанса на примере качелей.

Итак, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы, амплитуда колебаний становится наибольшей.

Таким образом, необходимо сказать, что совпадение частоты вынуждающей силы с собственной частотой колебаний системы и является резонансом.

За примерами резонанса ходить далеко не нужно. Оконное стекло, дрожащее с определенной частотой каждый раз, когда мимо проезжает трамвай или грузовая машина; дрожание струны музыкального инструмента после того, как мы прикоснулись к соседней струне, настроенной в унисон с первой, и т. п. — все это явления резонанса.

Зарядим конденсатор некоторым количеством электричества (рис.4, а) и замкнем его после этого на катушку индуктивности (рис.4, б). Конденсатор начнет немедленно разряжаться. Через катушку индуктивности потечет разрядный ток, а появление тока в катушке приведет к возникновению магнитного поля вокруг нее. При этом в катушке возникнет ЭДС самоиндукции, которая будет задерживать разряд конденсатора. Когда конденсатор разрядится, то ток в катушке не прекратится, так как он будет теперь поддерживаться ЭДС самоиндукции за счет энергии, запасенной в магнитном поле катушки во время разряда конденсатора. Этот продолжающийся ток перезарядит конденсатор в обратном направлении, т. е. та пластина, которая была прежде положительной, станет отрицательной, и наоборот (рис.4, в).

Рисунок 4. Свободные колебания. Вверху – электрические, внизу – механические.

После этого конденсатор снова начнет разряжаться, снова перезарядится (рис.4, г, д) и т. д. Колебания тока в контуре будут продолжаться до тех пор, пока вся электрическая энергия, сообщенная контуру при заряде конденсатора, не превратится в тепловую энергию. Это произойдет тем скорее, чем больше активное сопротивление контура.

Итак, разряд конденсатора через катушку индуктивности является колебательным процессом. Во время этого процесса конденсатор несколько раз заряжается и разряжается, энергия поочередно переходит из электрического поля конденсатора в магнитное поле катушки и обратно.

Рисунок 5. Колебания в колебательном контуре.

Колебания тока, имеющие место при этом разряде, носят затухающий характер (рис.6).

Рисунок 6. Затухающие колебания в контуре.

Частота колебаний при выбранных величинах емкости и индуктивности является величиной вполне определенной и называется собственной частотой контура. Собственная частота контура будет тем больше, чем меньше величины емкости и индуктивности контура.

Если в колебательный контур ввести источник переменного тока, частота которого совпадает с собственной частотой контура, то колебания в контуре достигнут наибольшей величины, т. е. будет иметь место явление резонанса.

Между электрическими и механическими колебаниями может быть проведена далеко идущая параллель.

В табл. 1 слева даны электрические величины и явления, а справа аналогичные им величины и явления из области механики применительно к нашей механической модели колебательного контура.

Аналогия электрических и механических величин

Электрические величины	Механические величины
Индуктивность колебательного контура	Масса шара;
Емкость колебательного контура	Гибкость пружин
Активное сопротивление контура	Механическое трение
Пластины конденсатора	Пружины
Заряд конденсатора	Деформация (сжатие и растяжение) пружин
Положительный заряд пластин	Сжатие пружины
Отрицательный заряд пластины	Растяжение пружины
Сила тока	Скорость движения шара
Направление тока	Направление движения шара
Электродвижущая сила самоиндукции	Сила инерции шара
Амплитуда (наибольшее мгновенное значение тока)	Амплитуда (наибольшее отклонение шара от положения равновесия)
Частота (число циклов в секунду)	Частота (число колебаний в се¬кунду)
Резонанс (совпадение частоты внешней ЭДС с собственной частотой конура)	Резонанс (совпадение частоты толчков вынуждающей силы с собственной частотой колебаний шара)

Различные моменты электрического колебания и соответствующие им моменты колебания нашей механической модели колебательного контура изображены на рис.4.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!